
Leetcode included a strangely easy medium-difficulty problem in their 2025 hiring prep sprint called 2043. Simple Bank System. The problem statement is:
You have been tasked with writing a program for a popular bank that will automate all its incoming transactions (transfer, deposit, and withdraw). The bank has
naccounts numbered from1ton. The initial balance of each account is stored in a 0-indexed integer arraybalance, with the(i + 1)thaccount having an initial balance ofbalance[i].Execute all the valid transactions. A transaction is valid if:
- The given account number(s) are between
1andn, and- The amount of money withdrawn or transferred from is less than or equal to the balance of the account.
Implement the
Bankclass:
Bank(long[] balance)Initializes the object with the 0-indexed integer arraybalance.boolean transfer(int account1, int account2, long money)Transfersmoneydollars from the account numberedaccount1to the account numberedaccount2. Returntrueif the transaction was successful,falseotherwise.boolean deposit(int account, long money)Depositmoneydollars into the account numberedaccount. Returntrueif the transaction was successful,falseotherwise.boolean withdraw(int account, long money)Withdrawmoneydollars from the account numberedaccount. Returntrueif the transaction was successful,falseotherwise.
Basically, you need to keep track of n bank accounts and do three kinds operations on them: deposit, withdraw, and transfer. The steps for deposit are:
- Ensure the account exists
- Add the amount of the deposit to the account
For withdraw:
- Ensure the account exists
- Ensure the account has enough money to cover the amount of the withdrawal
- Deduct the amount of the withdrawal from the account
For transfer:
- Ensure both accounts exist
- Ensure the source account has enough money to cover the amount of the transfer
- Deduct the amount of the transfer from the source account and add it to the target account
Honestly, this looks pretty simple.
When I saw this question, I was confused why it was marked medium-difficulty and not easy-difficulty. Normally, a medium-difficulty problem requires at least some data structures/algorithms knowledge and takes an experienced programmer between 10 and 15 minutes to complete. However, solving this problem looks trivial at first glance, since it only requires an array and a couple conditional statements. Anyone who has read the first chapter of a coding textbook should be able to tackle it. A simple C++ solution is:
class Bank
{
std::vector<long long> balance;
public:
Bank(std::vector<long long> &balance) : balance{balance}
{
}
bool transfer(int account1, int account2, long long money)
{
if (account1 < 1 || account1 > balance.size() ||
account2 < 1 || account2 > balance.size() ||
balance[account1 - 1] < money)
{
return false;
}
balance[account1 - 1] -= money;
balance[account2 - 1] += money;
return true;
}
bool deposit(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
balance[account - 1] += money;
return true;
}
bool withdraw(int account, long long money)
{
if (account < 1 || account > balance.size() || balance[account - 1] < money)
{
return false;
}
balance[account - 1] -= money;
return true;
}
};
I became even more suspicious after submitting my solution—which took me less than five minutes to write—and seeing it pass all the tests with 90th percentile efficiency. The discussion on this question is full of users just as confused as I was, questioning whether they missed something and if the problem truly deserves a medium-difficulty label.
It’s tempting to chalk this discrepancy up to a mistake by the difficulty assigners and move on, but it’s wiser to consider what this question is really getting at and to make sure we understand it. After thinking about this problem more carefully, I realized that a real interviewer wouldn’t be happy with the solution I wrote. They aren’t interested in assessing if you know how arrays work; they want to know how you reason about real-world problems, and the simple solution wouldn’t perform well in the real world. There’s no access control, logging, account routing, etc. which are essential for banking systems.
The most important missing feature, in my view, is transaction isolation, and I bet it’s the first thing an interviewer will want you to notice and implement. Banking systems typically take requests from many sources: tellers, ATMs, cash registers, apps, etc. In my simple solution, account balances are first read, then updated. If two operations come in at the same time, they might both update the original value rather than applying the updates in order. For example, an account with $100 might receive an ATM withdrawal of $100 at the same time that someone cashes a $100 check for the same account. The bank system starts processing the ATM withdrawal first and verifies that there’s enough money in the account. Before it deducts the amount, it starts processing the check. Since the ATM deduction hasn’t occurred yet, the system still thinks there’s enough money for the check as well. Then, it finishes processing both transactions, resulting in a negative balance of -$100 that shouldn’t be possible. This violates the principle of isolation, that transactions shouldn’t interfere with one another. Interference occurs in this case because the ATM deduction invalidates the check transaction after it already passed verification. A bug like this is catastrophic and can bankrupt a bank if exploited by a malicious actor.
There are many ways to guarantee isolation. The simplest is to serialize the transactions so that they run one at a time rather than all at once. We can guarantee this by wrapping Bank in a class that filters transactions from all the different sources and transforms them into an orderly queue, or by modifying the Bank class itself. However, this would result in a massive slowdown in performance—if we have millions of accounts, serialization would mean that we can’t transact on a single account while any of the others are in use. We need to be able to parallelize transactions across multiple accounts at once if we want to stay in business.
Mutual Exclusion
The simplest way to enable parallelization while ensuring isolation is to use mutual exclusion, which is simply to guarantee that an account can only be accessed by one thread of operation at a time. This means that a check transaction can’t occur while an ATM transaction is being processed. We can ensure mutual exclusion using mutual exclusion locks, which is a mechanism that can be held by exactly one thread. If we create a mutual exclusion lock for each account, and require threads to acquire an account’s lock before accessing it, then we can ensure mutual exclusion for the accounts themselves. Then, any concurrent transactions will be stalled until that thread releases the lock, which it will only do once it is done with the account. Here’s one way to implement this:
class MutexBank
{
std::vector<long long> balance;
std::vector<std::mutex> locks;
public:
MutexBank(std::vector<long long> &balance) : balance{balance}, locks(balance.size())
{
}
bool transfer(int account1, int account2, long long money)
{
if (account1 < 1 || account1 > balance.size() ||
account2 < 1 || account2 > balance.size())
{
return false;
}
locks[account1 - 1].lock();
if (balance[account1 - 1] < money)
{
locks[account1 - 1].unlock();
return false;
}
if (account1 == account2)
{
locks[account1 - 1].unlock();
return true;
}
locks[account2 - 1].lock();
balance[account1 - 1] -= money;
balance[account2 - 1] += money;
locks[account1 - 1].unlock();
locks[account2 - 1].unlock();
return true;
}
bool deposit(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
locks[account - 1].lock();
balance[account - 1] += money;
locks[account - 1].unlock();
return true;
}
bool withdraw(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
locks[account - 1].lock();
if (balance[account - 1] < money)
{
locks[account - 1].unlock();
return false;
}
balance[account - 1] -= money;
locks[account - 1].unlock();
return true;
}
};
If you submit this code on Leetcode, you will pass all of the tests—however, in a production setting, this code will eventually stop running because concurrent transfer calls can block each other due to a bug called deadlock. The list of operations in transfer looks like this:
- Acquire the lock for the source account
- Acquire the lock for the target account
- Transfer the amount from the source account to the target account
- Release the lock for the target account
- Release the lock for the source account
This will always work in a serialized environment like the one Leetcode uses for testing, because we release every lock that we acquire. Problems arise when multiple callers get involved, like in the real world where many different sources can send banking operations. I will isolate one problematic scenario to illustrate the point. Imagine that two friends (let’s call them Alex and Brett) try to transfer $20 to each other at the same time. One possible sequence of operations is the following:
- Alex acquires the lock for Alex’s account
- Alex acquires the lock for Brett’s account
- Brett tries to acquire the lock for Brett’s account and waits
- Alex transfers $20 from Alex’s account to Brett’s account
- Alex releases the lock for Brett’s account. As a result, Brett acquires the lock for Brett’s account
- Brett tries to acquire the lock for Alex’s account and waits
- Alex releases the lock for Alex’s account. As a result, Brett acquires the lock for Alex’s account
- Brett transfers $20 from Brett’s account to Alex’s account
- Brett releases the lock for Alex’s account
- Brett releases the lock for Brett’s account
In this case, the transfers worked as intended. The mutexes prevented Brett from accessing the accounts while Alex was using them, and both completed their transfers successfully. However, this won’t always be the case. Here’s an example of a sequence that deadlocks:
- Alex acquires the lock for Alex’s account
- Brett acquires the lock for Brett’s account
- Alex tries to acquire the lock for Brett’s account and waits
- Brett tries to acquire the lock for Alex’s account and waits
Since both transfers are waiting on the other transfer, neither can make progress. They are blocking each other—this is deadlock. The root cause of deadlock in our program is that a thread that already holds a lock tries to acquire another one during while executing the transfer function. When this happens, there is a chance that it will have to wait because another thread already holds that second lock. As long as it’s possible for a lock-holder to acquire additional locks, deadlock will be possible.
Fortunately, C++ provides us a way to acquire multiple locks at once. Rather than acquiring the source and target locks one at a time, we can make a single call to std::lock(source, target), which waits until both locks are available and then acquires both at the same time. This makes the deadlock sequence between Alex and Brett impossible since threads can either be waiting or holding locks, but never both. Brett will never hold a lock that Alex needs at the same time that Alex holds a lock that Brett needs.
Now that we’re acquiring multiple locks in one function call, we need to be sure we aren’t trying to acquire the same lock at the same time. This can happen if the source and target accounts in a transfer call are the same. To address this issue, we just need to move our early return when target==source to before we lock our source and target mutexes.
Whenever mutexes and locks are involved, we need to be careful that our code can’t end up deadlocked. In concurrent programming, we say that lock-containing code is blocking, which is the weakest progress guarantee. Any code that is blocking provides no guarantee that progress will be made. Since deadlock only occurs under certain circumstances, it can be hard to identify the source of a deadlock bug. It’s common to have concurrent code that works fine most of the time, but very rarely freezes due to deadlock. In this case, we were able to detect the bug using the heuristic that lock holders shouldn’t try to acquire additional locks. Other cases of deadlock are harder to notice.
The raw mutexes I used in MutexBank are prone to a common kind of deadlock that’s caused by developer error. Note that every time we return from our functions, we need to release the mutexes we acquire by calling .unlock(). If we don’t do this, the mutex will be permanently stuck in a held state because its holder will no longer exist. Ensuring that the mutexes are always released is already getting unmanageable in the transfer function due to all the conditional returns. Even experienced developers struggle to manage mutex states, especially if the code makes exception-throwing calls or has the potential to throw exceptions itself.
This issue might remind you of a similar problem with memory management. In C and C++, we need to free any memory that we acquire, or else that memory will stay reserved forever. Eventually, all of this un-freed extra memory will cause the program to slow down and crash. C++ makes memory deallocation easier by introducing deconstructors, which are automatically called whenever an object exists scope. All of the calls to free memory can be put in the deconstructor so that memory deallocation will be handled automatically. The pattern of using deconstructors to automatically release acquired resources like memory is called Resource Management Is Initialization, or RAII.
RAII is most commonly used to manage memory, but the pattern applies to any resource that needs to be acquired and released. We can extend RAII to mutexes by using constructors to acquire the mutex and deconstructors to automatically release acquired mutexes. The C++ standard library makes RAII for mutexes easy by providing std::lock_guard(), which simplifies the process of automatically acquiring and releasing mutexes to a single function call. After we fix the deadlock bug and introduce RAII to MutexBank, we get the following:
class MutexBankV2
{
std::vector<long long> balance;
std::vector<std::mutex> locks;
public:
MutexBankV2(std::vector<long long> &balance) : balance{balance}, locks(balance.size())
{
}
bool transfer(int account1, int account2, long long money)
{
if (account1 < 1 || account1 > balance.size() ||
account2 < 1 || account2 > balance.size())
{
return false;
}
std::scoped_lock lock(locks[account1 - 1], locks[account2 - 1]);
if (balance[account1 - 1] < money)
{
return false;
}
if (account1 == account2)
{
return true;
}
balance[account1 - 1] -= money;
balance[account2 - 1] += money;
return true;
}
bool deposit(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
std::lock_guard lock(locks[account - 1]);
balance[account - 1] += money;
return true;
}
bool withdraw(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
std::lock_guard lock(locks[account - 1]);
if (balance[account - 1] < money)
{
return false;
}
balance[account - 1] -= money;
return true;
}
};
Lock-free programming
Although MutexBankV2 solves some of the potential deadlocks in MutexBank, it still only provides the blocking progress guarantee. No matter how reliable we make our software, one of our threads could randomly crash or freeze while holding a mutex and block all the other threads who need that mutex. A typical situation where this occurs is when the thread scheduler consistently favors other threads, preventing the thread holding the mutex from running and causing it to “starve.” To avoid this kind of deadlock, we can upgrade our progress guarantee to be lock-free. At least one thread in a lock-free program will always make progress, so deadlock cannot occur.
To make our banking system lock-free, we need to write our code without using any mutexes. Instead, we will optimistically update values, and roll-back our update if we detect a conflict caused by interference with other threads. The core of most lock-free programs is the Compare-And-Set loop, which uses atomic variables that make it possible to read and update values in a single step. When we update a value, we will first check that the value we want to update hasn’t been modified by anther thread. Then, if the old value is what we expect, we set it to the new value. If the old value is something else (because another thread changed it), we try again. To implement our banking system with CAS loops, we first need to replace our account balances with atomic variables that support the compare and set operation:
std::vector<std::atomic_llong> balance;
FinalBank(std::vector<long long> &balance) : balance(balance.size()), locks(balance.size())
{
for (size_t i = 0; i < balance.size(); ++i)
{
this->balance[i].store(balance[i]);
}
}
A CAS loop version of the withdraw function looks like this:
bool withdraw(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
auto old = balance[account - 1].load();
while (
old - money >= 0 &&
!balance[account - 1].compare_exchange_strong(old, old - money)) {}
return old - money >= 0;
}
After we verify that the account exists, we try to withdraw from it until either the account balance is too low or the withdrawal succeeds. The withdrawal succeeds if the amount we read before the update attempt, old, matches the amount we see when we attempt to withdraw. If another thread changes the balance between when we read the value and do the comparison, then old will be updated to the new current balance and we try again. Since compare_exchange_strong is atomic, the whole process of checking the updated value and making the subsequent exchanges cannot be interfered with. This means that interference cannot occur at any point in the withraw function.
If our banking system only had the deposit and withdraw functions, the CAS loop would be all we need. However, the transfer function cannot be implemented with CAS loops alone, since they can only update one value at a time. If we tried to implement transfer with CAS loops, there would be a small period in between our two account balance updates where the banking system would not be in a valid state and we would lose isolation. To see this more clearly, imagine we wrote the following lock-free version of transfer:
- CAS loop to withdraw X dollars from the source account
- CAS loop to deposit X dollars in the target account
If someone looked at the banking system between steps 1 and 2, they would see X dollars missing from both the source and target accounts. The double amount missing means that there are X dollars unaccounted for in the banking system. This kind of bug is called read skew and is commonplace in distributed systems. In general, read skew is the phenomenon where it is possible to see the intermediate results of an incomplete operation. To avoid read skew, transfer must be all-or-nothing: either we see the state of the accounts before the transfer, or we see the state of the accounts after the transfer.
An earlier version of our banking system had this all-or-nothing property—the version we made using mutexes. However, that version didn’t leverage CAS loops to make deposit and withdraw wait-free. Ideally, we want to only use mutexes when we transfer money between two accounts, and otherwise use CAS loops for everything else (withdrawals and deposits). We can do this using std::shared_mutex, which can be held by multiple threads in its shared mode, but only one thread in its unique mode. Shared mutexes are commonly used when some variable has many readers and just a few writers. Since reading doesn’t modify any data, the readers can all access the variable at the same time. When a writer wants to modify the data, it will first wait for all the readers to release the shared mutex, and then it will prevent both readers and writers from acquiring the shared mutex until it releases. For our purposes, transfer will work like a writer, while withdraw and deposit will act like readers. When only withdraw and deposit are called on account, all the threads will be able to access it without waiting. However, a transfer call on that account will force all the other threads out which will prevent the account’s data from access while the transfer is processed.
Now, we have all the tools we need for the final version of our banking system. When we want to lock a shared mutex in shared mode, we use a std::shared_lock RAII object, and when we want to lock a shared mutex in unique mode, we use std::unique_lock. This gives us the final banking system:
class FinalBank
{
std::vector<std::atomic_llong> balance;
std::vector<std::shared_mutex> locks;
public:
FinalBank(std::vector<long long> &balance) : balance(balance.size()), locks(balance.size())
{
for (size_t i = 0; i < balance.size(); ++i)
{
this->balance[i].store(balance[i]);
}
}
bool transfer(int account1, int account2, long long money)
{
if (account1 < 1 || account1 > balance.size() ||
account2 < 1 || account2 > balance.size())
{
return false;
}
std::scoped_lock lock(locks[account1 - 1], locks[account2 - 1]);
if (balance[account1 - 1] < money)
{
return false;
}
if (account1 == account2)
{
return true;
}
balance[account1 - 1].fetch_sub(money);
balance[account2 - 1].fetch_add(money);
return true;
}
bool deposit(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
std::shared_lock<std::shared_mutex> lock(locks[account - 1]);
balance[account - 1].fetch_add(money);
return true;
}
bool withdraw(int account, long long money)
{
if (account < 1 || account > balance.size())
{
return false;
}
std::shared_lock<std::shared_mutex> lock(locks[account - 1]);
auto old = balance[account - 1].load();
while (
old - money >= 0 &&
!balance[account - 1].compare_exchange_strong(old, old - money))
{
}
return old - money >= 0;
}
};
Note that in transfer and deposit, we use fetch_add and fetch_sub to add and subtract from account balances rather than CAS loops. fetch_add and fetch_sub update an atomic variable without checking their values first. We can use them in transfer and deposit because these operations don’t depend on the previous balances of the accounts they touch. After all these changes, we have arrived at a concurrent banking system that preserves transaction isolation while using a minimal amount of locks and while avoiding deadlock. This is the sort of work this Leetcode question wants you to do, and all the additional complexity from dealing with concurrency is what makes it Medium and not Easy.
Measurements
To wrap everything up, I will take some measurements of our banking system’s performance so we can see how the theoretical improvements I made play out in practice. Even though my focus in this article has been on progress guarantees and avoiding deadlock, it’s worthwhile to remember that the original reason we are dealing with concurrency at all is to improve on the performance of a serial banking system.
To test the banking system performance, I set up a simple testing apparatus that calls withdraw, deposit, and transfer 10,000 times for each account in the banking system. For the serialized banking system, all of these operations will run on the same thread. For the concurrent versions, I will spin up a thread for each account and divide the work evenly between them. Then, I will measure how long it takes for each banking system to process all these operations.
Since the performance testing results are inherently non-deterministic, I ran the testing apparatus 30 times for each of the banking system versions I was interested in: the original, serial-only Bank, the deadlock-free MutexBankV2, and the partially wait-free FinalBank. After I run the test, I plotted my measurements using boxplots, which let us compare the average performance and the performance variance of our different systems. This is the plot I got when the banking systems have 10 accounts:
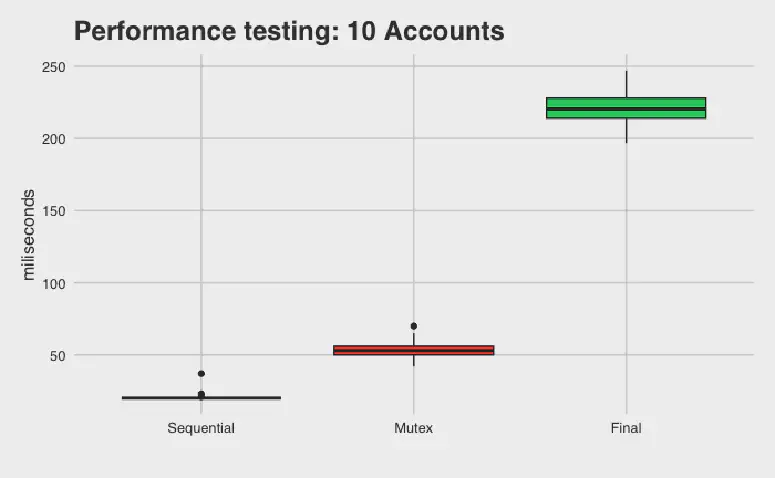
Figure 1: Time taken for banking systems with 10 accounts.
Interestingly, the serialized banking system runs much faster than either of the concurrent versions. This is because concurrency isn’t free—the CPU will have to take some time to spin up all the extra threads. We also don’t get perfect speedup because the threads will contend with each other when they are trying to process the same account. When the number of operations are small, the benefit from dividing the work between multiple threads is overwhelmed by the cost of spinning them up. We start to see profit from parallelization when we increase the number of accounts to 100:
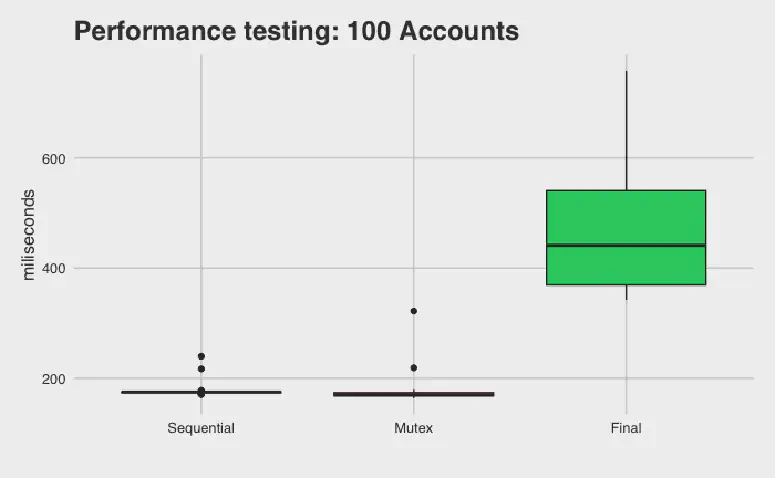
Figure 2: Time taken for banking systems with 100 accounts.
With 100 accounts, MutexBankV2 runs faster than the serialized bank. However, FinalBank is still running slower. Let’s increase the number of accounts to 1,000:
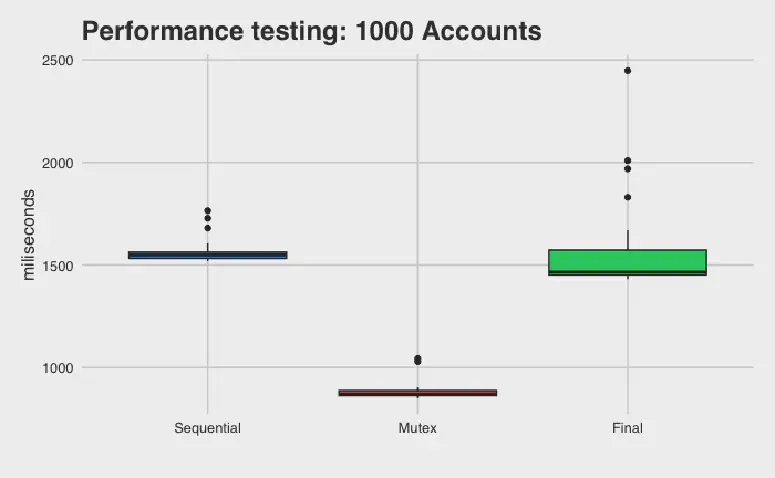
Figure 3: Time taken for banking systems with 1,000 accounts.
Now, MutexBankV2’s relative performance is skyrocketing and FinalBank’s performance is finally approaching the performance of the serialized bank. However, FinalBank still runs slower then MutexBankV2. How is this possible? FinalBank was supposed to be faster than MutexBankV2 because it never blocks, but our data says otherwise. This illustrates a key principle in performance engineering: never guess about performance. Oftentimes, theoretical improvements are practically harmful due to hardware intricacies and other hidden factors that are hard to account for. In this case, FinalBank’s performance is hurt by its use of atomic variables, which can be much more computationally expensive compared to non-atomic variables. To make a variable atomic, the compiler will have to introduce locks or some other way to manage access, which incurs a performance penalty. Even if we remove all transfer calls, leaving only the deposit and withdraw calls that FinalBank is optimized for, it still performs worse than MutexBankV2:
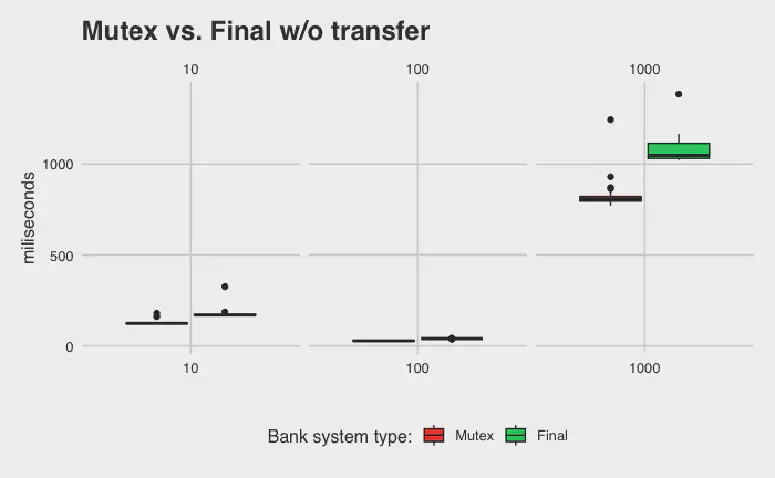
Figure 4: Comparing MutexBankV2 and FinalBank without any transfer calls.
However, this doesn’t mean that FinalBank is useless. If we run our banking system in an environment where threads are prone to freeze, such as if our connection to our clients was unreliable, then it might be comforting to know that a failure in one thread won’t cascade to block the others. When we design systems, we need to consider the tradeoffs between our different requirements, rather than tunnel visioning on optimizing for a single metric. In this case, we might choose FinalBank to trade performance for reliability. It’s not too hard to imagine a situation where we take this trade—after all, we are designing a banking system, and operating an unreliable banking system is literally gambling with our customer’s money.
Conclusion
All of the stuff I brought up in this post would be covered in an undergraduate-level parallel computing course. For me, that course was called CMSC 23010, and it was taught by the absolute genius Professor Hank Hoffman. The projects in this course were very similar to the investigation I did here with the banking system—given some kind of task, we had to design different serial and parallel algorithms to complete the task, then measure the performance of our algorithms.
But early on in the course, I realized that the grader wasn’t actually running any of our code to verify our measurements. Now, I never totally blew off an assignment, but I wasn’t the best programmer back in the day and my programs had a ton of memory leaks that would make my tests take much longer to run than they should. Rather than fixing my bugs, I would just run my programs overnight and hope that when I woke up, I would have some usable measurements rather than an error screen. This janky setup served me well except that the long runtimes made it impossible to take multiple measurements, so I sometimes had some weird results where something that was supposed to be fast would run slower than something that was supposed to be slow. Whenever this happened, I would just add a couple lines to my writeup that I got some weird result and that I had no idea how this happened. Somehow, the grader always accepted this and didn’t dock me any grades for messing up the measurement process.
The year after I took the course, I received an email from Professor Hoffman asking if I wanted to grade the next term of CMSC 23010. I really didn’t feel confident about the job given that I didn’t do the class the right way when I took it myself, but I said yes anyways. I took a similar approach to grading as my predecessor—I was very lenient with my standards and didn’t run any of the code. I think Professor Hoffman didn’t care too much that basically everyone was getting perfect marks because about a third of the class dropped in the first two weeks. I do remember that during the last week of the class, someone who skipped one of the earlier projects asked me if he could submit it now for points. I said sure and gave him full marks.
My CMSC 23010 misadventures were fun at the time, but I fear they distracted me from actually learning parallel computing the right way. I never really developed a good intuition for many key concepts like consistency models, progress guarantees, and the conditions that make deadlock/race conditions possible. Like many topics in computer science, parallel computing/concurrency is something learned best through practice.
In one way, this blog post is a deep dive into an interview question. In another, it is making up for lost time. Many years after CMSC 23010, I’m finally writing some correct concurrent programs and taking statistically sound measurements. In the process, I feel like I finally have a firm grasp on many of the concepts that I previously only knew at a theoretical level. I hope this post has been informative, and I encourage you to work through this exercise yourself. Also, if you have ideas for improving the banking system design, please let me know! It’s fun to do little toy projects like this and I plan on tinkering more with it if new things come up. Thanks for reading yayyyyyyyy!!!! ■


