
Risk management is critical for speedrunning Minecraft, the world’s most famous procedurally-generated video game. Every requirement for completing the game is based on luck. When you start the game, you must hope to spawn near a structure that gives you enough resources to last you for the rest of the run. In the Nether, you must first find a Bastion within a couple hundred blocks, then find a Nether Fortress near the Bastion. To finish the run, you need to get lucky finding the End Portal and get then get a good Dragon fight pattern to beat the game. All of these are determined by RNG and cannot be influenced by the player. So, speedrunners have developed a deep understanding of the game’s world generation and the relevant probabilities to squeeze out every drop of luck they can get from their runs. However, much of this information is unavailable on the open web (e.g. on forums or the Minecraft Wiki) and can only be learned by talking to experienced runners. In this post, I will show how some of Minecraft’s best speedrunners discovered the odds for one of these critical probabilities, an effort that turned out to be far more complex than I had anticipated.
The probability that caught my eye comes from Feinberg’s exhibition run at the 2024 GSA Speedrun Summit, where he was trying to find a Nether Fortress after completing all of his tasks in a Bastion. However, the signal he followed, hoping it would lead him to a Nether Fortress, had instead led him to a useless, second Bastion. Normally, he would restart his game after something like this, but since he was doing an exhibition, he was forced to power on. Couriway, the commentator for the run, explained that the chance of finding a Bastion rather than a Nether Fortress is “about 20%,” making Feinberg’s bad luck quite the anomaly. But then Feinberg follows up Couriway’s comments by noting that Bastions have a 60% chance of spawning compared to 40% for Nether Fortresses. These conflicting statements confused me. If Feinberg was right, then he wasn’t unlucky at all—actually, finding a Bastion is the expected result. So, I set upon the task of figuring out who was right by calculating the probability of finding a second Bastion from the ground up.
Feinberg’s run at GSA Speedrun Summit 2024. Couriway is sitting behind him and commentating the run.
To understand how Couriway got his 20% figure, we first need to examine Feinberg’s speedrunning strategy and the signal he was trying to use. To beat Minecraft, Feinberg needs to complete the End Portal using ender eyes, and in order to craft those ender eyes, he needs to collect blaze rods. Since blaze rods can only be obtained from Nether Fortresses, an un-skippable part of Feinberg’s run involves finding a Nether Fortress, which spawns in the Nether. The Nether is divided into a grid of 368×368 block regions, and in each region, either a Nether Fortress or a Bastion can spawn. Since Feinberg only cares about Nether Fortresses, any region that contains a Bastion is useless and means he has to travel hundreds of blocks to reach the next region. Each region is too large to search from the outside, so Feinberg will need to search through each region on foot to check if it contains a Nether Fortress or a Bastion.
To make his search easier, Feinberg relies on a technique called pieray, which exploits Minecraft’s debug menu to scan for mob spawners in a certain area. If he does everything correctly, the pieray will lead him to the closest region with a mob spawner, and since Nether Fortresses contain blaze spawners, this signal possibly indicates that a region has a Nether Fortress. However, certain Bastions, called “Treasure Bastions”, can also trigger the pieray because they contain magma cube spawners. This is the false positive that Feinberg ran into at the 2024 GSA Speedrun Summit.
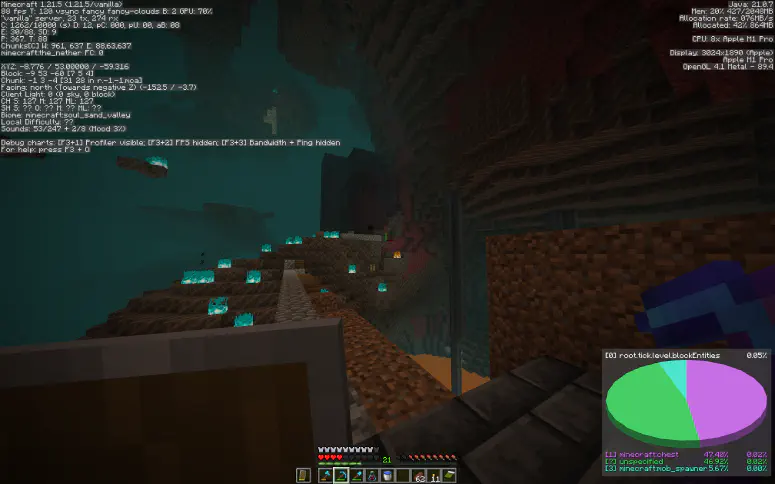
Me using pieray in my own Minecraft world. If you look carefully, you will see a Nether Fortress in the background and the label ‘mob_spawner’ in the bottom right.
Even with the information from pieray, the probability of mistakenly finding a Bastion won’t drop to 20%. With a 60% base chance for a Bastion to spawn and three out of four Bastions ruled out due to pieray, we expect the probability of a Treasure Bastion given a hit on the pieray to be closer to 30%. In order to reach 20%, something would need to be suppressing the spawn rate of Treasure Bastions. One possibility is that the Bastion base rate is lower than 60%. Another is that Treasure Bastions spawn less frequently than other Bastion types. Or, Feinberg and Couriway could be wrong about the figures they’re citing. To get to the bottom of this, we will need to calculate this probability ourselves, working through the same steps that Couriway worked through to get his 20%.
The number we are looking for is the conditional probability of a structure being Treasure Bastion, given that we know it contains a spawner. Using Bayes’ Theorem, we have the probability:
\[ \begin{aligned} P(\text{Treasure Bastion}|\text{Spawner})&= \\ \frac{P( \text{Spawner} |\text{Treasure Bastion})P(\text{Treasure Bastion})}{P(\text{Spawner})} \end{aligned} \]Since spawners can only appear in Nether Fortresses and Treasure Bastions, we can rewrite the probability of a spawner as \(P(\text{Spawner})=P(\text{Nether Fortress})+P(\text{Treasure Bastion})\). We also know that all Treasure Bastions contain spawners, so we can rewrite the conditional probability of a spawner given a Treasure Bastion as \(P(\text{Spawner}|\text{Treasure Bastion})=1\). This gives us the simplified probability:
\[ \begin{aligned} P(\text{Treasure Bastion}|\text{Spawner})&= \\ \frac{P(\text{Treasure Bastion})}{P(\text{Nether Fortress})+P(\text{Treasure Bastion})} \end{aligned} \]Now, all we need to do is figure out the spawn rate of Treasure Bastions and Nether Fortresses. Feinberg said that the spawn rate of a Nether Fortress is 40%, so it’s tempting to plug it in. However, we already suspect that there’s something affecting spawn rates, so it’s a good idea to double-check. A big clue appears on the Minecraft wiki page for Nether Fortress, which says that
The chance of a fortress attempting to generate instead of a bastion is 2⁄5 (40%) in Java Edition […] However, if a bastion attempts to generate in the basalt deltas, a fortress generates instead, resulting in fortresses being the most common in the basalt deltas.
Aha! While Feinberg was right that Bastions have a base 60% chance to spawn, it turns out that the Bastion base spawn rate is suppressed. The adjusted probability of a Nether Fortress spawn is \(P(\text{Nether Fortress})=\frac{2}{5}+\frac{3}{5}P(\text{Basalt Delta})\). If we check the Basalt Delta wiki page, we find out that “The basalt deltas is the second rarest Nether biome, making up around 16% of the Nether by volume.” So, we find that:
\[ \begin{aligned} P(\text{Nether Fortress})&=\frac{2}{5}+\frac{3}{5}0.16 \\ &=0.496 \end{aligned} \]Now, we only need to verify that Treasure Bastions have an equal likelihood to spawn as the other Bastion types. The Bastion wiki page, however, doesn’t provide a breakdown of the spawn rates for each Bastion type, and people online have no idea either. So, we will have to figure this out by ourselves.
My first idea was to take a sample of all the structures that generate in the Nether and count how many of them are Treasure Bastions. I used the Bastion locator Chunkbase app to produce a map containing 1,000 Bastions and asked ChatGPT to count how many Bastions of each type there were.

The map of Bastion types I got from Chunkbase.

ChatGPT’s count of the Bastion types.
Unfortunately, there was too much noise in the map for ChatGPT to produce an accurate count of each Bastion type. Even without the noise, the counts had such high variance that I would need to take many samples to be confident in my probability measurement—something I couldn’t afford due to my low ChatGPT quota.
The next thing I tried was to find the code that generated the Bastions and see if it contained information about the spawn probabilities. While Minecraft isn’t an open-source game, I knew that it had a large modding scene which suggests that people were somehow able to access the game’s code. A quick search online led me to MCP-Reborn, a project dedicated to decompiling the Minecraft source code. I knew that a lot of the code would still be obfuscated, but I hoped that enough would be labelled for me to deduce how Bastion generation works. With this in mind, I cloned the repo, built the project, and started hunting for the information I needed. After digging around for some time, I found this snippet of code that initializes a Structure spawn pool with four Bastion types:
new StructureTemplatePool(
holder1,
ImmutableList.of(
Pair.of(
StructurePoolElement.single("bastion/units/air_base",
holder),
1),
Pair.of(
StructurePoolElement.single("bastion/hoglin_stable/air_base",
holder),
1),
Pair.of(
StructurePoolElement.single("bastion/treasure/big_air_full",
holder),
1),
Pair.of(
StructurePoolElement.single("bastion/bridge/starting_pieces/entrance_base",
holder),
1)
),
StructureTemplatePool.Projection.RIGID
)
While I can’t be sure yet, it looks like this snippet associates each type of Bastion with an integer weight of 1 and puts them into a list. If this is true, then all the Bastion types would have the same chance of spawning. To confirm my hypothesis, I tried to find where this list of pairs was used. Eventually, I came across a snippet that transforms the list of StructurePoolElement/integer pairs from the original StructureTemplatePool into a flat list containing only StructurePoolElements—each one repeated according to its associated integer value:
public StructureTemplatePool(Holder<StructureTemplatePool> p_255747_, List<Pair<StructurePoolElement, Integer>> p_255919_) {
this.rawTemplates = p_255919_;
this.templates = new ObjectArrayList<>();
for (Pair<StructurePoolElement, Integer> pair : p_255919_) {
StructurePoolElement structurepoolelement = pair.getFirst();
for (int i = 0; i < pair.getSecond(); i++) {
this.templates.add(structurepoolelement);
}
}
this.fallback = p_255747_;
}
When the game generates a structure from this pool, it makes a random draw from the new, flattened list:
public StructurePoolElement getRandomTemplate(RandomSource p_227356_) {
return (StructurePoolElement)(this.templates.isEmpty() ?
EmptyPoolElement.INSTANCE :
this.templates.get(p_227356_.nextInt(this.templates.size())));
}
This was enough evidence to convince me that each Bastion type has an equal spawn probability. Now, we can calculate:
\[ \begin{aligned} P(\text{Treasure Bastion})&=P(\text{Bastion})P(\text{Treasure Bastion}|\text{Bastion}) \\ &=(1-P(\text{Nether Fortress}))\frac{1}{4} \\ &=\frac{1-0.496}{4} \\ &=0.126 \end{aligned} \]Then, we can plug all of this back into our original probability and get the conditional probability of a Treasure Bastion given we detect a spawner:
\[ \begin{aligned} P(\text{Treasure Bastion}|\text{Spawner})&=\frac{P(\text{Treasure Bastion})}{P(\text{Nether Fortress})+P(\text{Treasure Bastion})} \\ &=\frac{0.126}{0.126+0.496} \\ &=0.2025 \\ &=20.25\% \end{aligned} \]So, accounting for Basalt Deltas, pieray, and the Bastion type distribution, we finally get Couriway’s 20%. When I started writing this post, I thought I was disproving Couriway’s statement, not proving it. My first calculation for the probability of finding a Treasure Bastion was 10%, and my second calculation was 27%. I only found out about the Basalt Delta adjustment when I went to the Minecraft wiki to pull a quote for the 40%/60% spawn chance fact. I was so disappointed to find out that after I accounted for Basalt Deltas, the probability of finding a Treasure Bastion ended up being 20.25%, almost exactly what Couriway said in his commentary. Well, whatever now we all know how this calculation is done and also that we should just trust the professional speedrunners when they spout off facts about Minecraft after all they’re playing this chungus game for ten hours every day. ■


